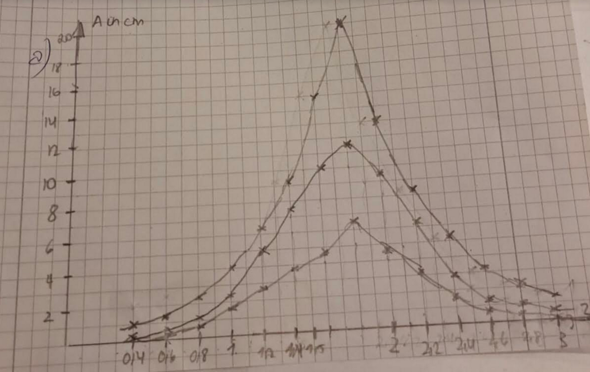
Genau genommen hängt die Frequenz der größten Amplitude ein wenig von der Dämpfung ab. Das Maximum sollte sich bei starker Dämpfung also ein wenig nach links verschieben, gemäß der Formel \( \omega_{gedämpft} = \sqrt{\omega_{ungedämpft}^2 - \delta^2 } \)
wobei \( \delta \) der Dämpfungsfaktor aus der Formel \( y(t) = A\cdot e^{-\delta t} \cdot sin(\omega t) \) ist.
Punkte: 2.65K
Die oberste Kurve zeigt die Resonanzkurve bei der kleinsten Dämpfung, die untere Kurve bei der größten Dämpfung.
Bei großer Dämpfung sollte das Maximum gemäß obiger Formel etwas nach links verschoben sein. Bei eurem Versuch war aber die Dämpfung so schwach, dass diese Verschiebung nicht sichtbar ist.
Aber eine Bitte: Informiere dich anhand von Büchern oder Internet über das Thema Resonanz und Resonanzkurven. Es ist nach meiner Einschätzung nicht sinnvoll, wenn ihr im Unterricht Versuche macht und Kurven aufnehmt, wenn deren Grundlagen nicht bekannt sind. Wurde es im Unterricht denn nicht erklärt, was hier geschieht?
─ stefriegel 11.06.2023 um 12:04